这是给自己看的描述统计学笔记,第五课标准化,Standardization.
上一节课还在说只停留在初中水平,这一课难度突增就变成高三的内容了。
这一课回答的问题是,“怎样比较两堆相似但不相同的数据?”
Score, Absolute Frequency 与 Percentage
对于一个路人来说,怎样的描述才能最容易最直观地知道一个学生考试后的结果如何呢?
- 这次期末我总分 505.
- 这次期末我全级排名 105.
- 这次期末我比全级 85% 的学生都要高分。
三个说法都没有错误,但是包含的信息却有所不同:
- 第一个说法 (Score) 还需要知道满分是多少才可以知道得分率,而且还无法与其他人的得分率进行比较,还需更多信息。
- 第二个说法 (Absolute Frequency) 还需要知道全级的人数才能知道学生表现如何。
- 第三个说法 (Percentage) 虽然省略了真实的得分或者排名,然而比 85% 的学生都要高分就可以得知这个学生的水平其实不错。
可以看出,用百分比来衡量某个数字在一堆数据或者说一个分布当中的位置更加直观:
- 不需要额外的数值。
- 许多不同的分布都能标准化 Standardized 成为百分比,这样就能比较不同的分布,例如说另一个学校的某个学生在其学校的水平,与上面那个学生在其学校的水平。
Histogram 与 Model
如此说来,计算出一个数值在整个分布当中的百分比,能让路人很快明白这个数值的位置在哪。
要计算这个百分比或者说位置,当然可以按顺序或者倒序来排列,然后看看比它大或者比它小的数据所占整堆数据的百分比是多少;这是最原始的计算方法。
有些时候不需要那么精准的时候可以看这堆数据的 Histogram 来估计。下面是 200 个经常锻炼的成年人当中 88 个男性的身高 histogram:
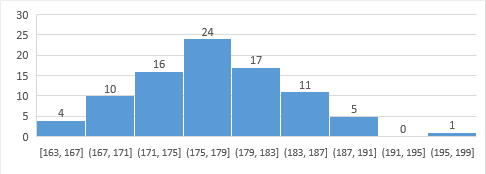
X 轴为身高,Y 轴为该身高区间的人数。例如说,一个 180cm (在 (179,183] 区间的左端)身高的男子在这当中,就会比 54 个人还要高,或者说比 61% 的人都要高。
身高 180cm 碰巧能在这个图表看出来,如果换成 181cm 就看不出来了,因为上面的图表用 4 作为 bin size. 当然把 bin size 减小能看出 181cm 所处的位置:
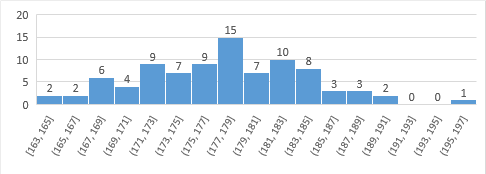
正如上图所示,181cm (在 (181,183] 区间的右端)身高会比 69% 的人都要高了。
这样计算未免有些麻烦,要得知一个数字在一堆数据当中的位置还要不断相应调整 bin size. 所以为了不用每次调整,histogram 可以用一条曲线来替代,或者说用一个 model 来替代真实的数据,这样来更加方便地看出一个数值在一堆数据当中的位置:
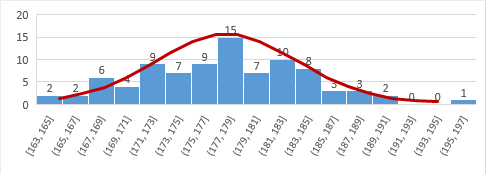
这条曲线下面的面积是 100%,表示其覆盖了所有的数据。一个数值在其中的位置,可以用其左方的面积来表示;例如,身高 181cm 的人左端的面积是 69%, 这是上面计算的数据。
如何通过这样的曲线来计算这个 percentage 将会是下一课讨论的内容,目前需要明白一堆数据的分布可以用一条曲线的模型去模拟去代表,通过研究曲线模型来推断本来数据的分布就可以了。
Distribution, Normal Distribution 与 Standard Normal Distribution
上面的这条曲线模型,其实叫做 Distribution 的曲线。Distribution 就是一堆数据的分布,而这条曲线就是模拟在各种 bin size 下这个分布的形状。
而 Normal Distribution, 则指看起来中间大两头小而且还是几乎左右对称的 Distribution:
这个时候 mean, median 和 mode 理论上是相等的。其实很多现实的分布,例如一堆人的身高、体重、收入程度,甚至是某次考试的分数,基本上都是 Normal Distribution.
然而 Normal Distribution 并不能适应所有分布。在第二课当中也提起过,分布还会有 positive skewed 与 negative skewed 的;例如说世界上所有国家按照核武器拥有数量从小到多来排列的话,就会出现拥有量为 0 的国家数量很大,然后就是少数拥有核武器的国家:
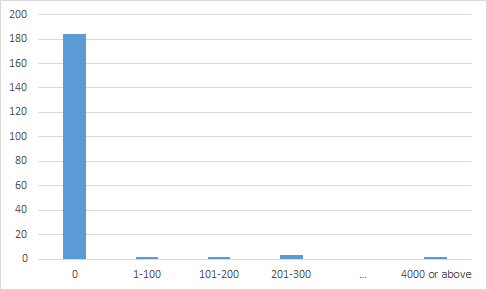
这是明显的 positive skewed distribution, Normal Distribution 的性质并不适用在这里。
而在这个对称的 Normal Distribution 当中,其中有一种情况是 mean 为 0 的同时 Standard Deviation 为 1 的情况。这个被称为标准正态分布,Standard Normal Distribution. 至于为何,下面将会进行解说。
如何比较两个不同的 Normal Distribution
考虑以下的情景:
A: 我这次语文考差了,全级平均分 70 分我只有 60 分啊。
B: 我的数学才叫差啊,全级平均分 60 分我只有 45 分啊。
问题来了,究竟是 A 的语文比较差,还是 B 的数学比较差?
当然 A 的语文达到平均分的 60/70=86% 也和平均分相距 10 分,B 的数学只达到平均分的 45/60=75% 也和平均分相距 15 分,无论是从比例还是从与平均分的差距来说 A 都看起来差一些。
不过,这样并不能下定论 A 的语文全级排名就会比 B 的数学全级排名要好;或者说,比 A 的语文成绩要差的人在全级的百分比,和比 B 的数学成绩要差的人在全级的百分比,不一定更高。单纯看平均分与实际分数并不是判断排名的唯一依据;分数这种通常符合 Standard Distribution 的数据,还需要考虑标准差 Standard Deviation.
语文和数学的难度不一样这个很容易发生。如果语文考试的试题区分度小些——或者说 Standard Deviation 比较小分数比较集中,例如说是 5 分;同时数学考试的试题区分度大些——或者说 Standard Deviation 比较大分数比较分散,例如说是 10 分,那么用上面的信息来看:
- A 的分数 60 分,和平均分 70 分相差 10 分,也就是 2 个 Standard Deviation (5 分)
- B 得分数 45 分,和平均分 60 分相差 15 分,也就是 1.5 个 Standard Deviation (10 分)
还记得上一课所说的 Standard Distribution 当中,一个数值掉进距离 mean 不同位置的概率或者说可能性:

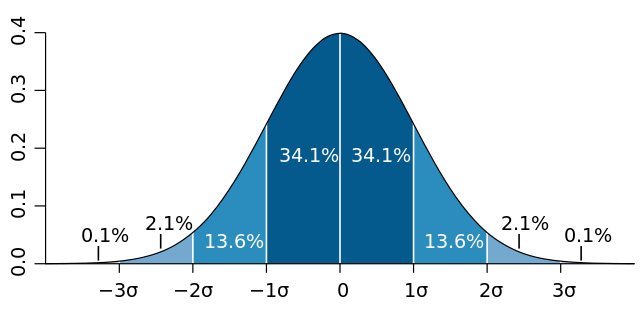
(这个维基百科的图真是百用不厌)
深蓝区域是距平均值小于一个标准差之内的数值范围,在正态分布中,此范围所占比率为全部数值之68%;两个标准差之内(深蓝,蓝)的比率合起来为95%;三个标准差之内(深蓝,蓝,浅蓝)的比率合起来为99.7%。
A 的分数已经是在距离 mean 两个 Standard Deviation 之外,只比大概 2.2% 的人成绩要好;而 B 的分数在距离 mean 1.5 个 Standard Deviation 的地方,至少没有 A 的成绩那么糟糕,尽管看起来分数什么的都要差。
这个“一个数值与 mean 之间相差了多少个 Standard Deviation”的数字,叫做 z; 或者说,一个数值和 mean 相差了 z 个 Standard Deviation. 当然 z 越大,数值与 mean 相差越远。
所以说,一个数值在一堆数据当中的位置通过其所处的 percentage 来判定。这个 percentage 是根据这个数值在这个 Distribution 的 x 轴的位置来判定(至于怎样计算,以后的事)。这个 x 轴的位置是根据数值与 mean 的距离来判定。这个距离是根据数值与 mean 相差多少个 Standard Deviation 来判定。
换句话说,现在只需要比较而不需要具体位置的 percentage 的话,只需要知道 z 的数值就可以了。
Standard Normal Distribution
第二次出现这个词语,其实刚才在比较分数的时候我们已经进行了一次对 Normal Distribution 进行 Standardization 标准化的过程了。
所谓的 Standardization, 就是比较不同 Distribution 当中,各自的一个数值 x 与 mean 相差了多少个 Standard Deviation, 也就是比较不同 Distribution 当中各自一个 x 的 z 是多少。通过将 x 转换为(标准化为)z 来比较本来不能直接比较的 x.
既然是 x 转换为 z, 那么将本来的分布用 z 来表示再次放在 x 轴重新绘制一条曲线的话,就能得出上面所说的 Standard Normal Distribution 的性质:
- Mean 为 0: Standardization 之前,Normal Distribution 中间的位置是 x=μ, 也就是 x 轴上 μ 的位置。而 Standardization 之后,这个新的 Standard Normal Distribution 中间的位置就变成了本来的 mean 的 z 值,也就是本来的 mean 与 mean 相差多少个 Standard Deviation, 也就是 0 个。
- Standard Deviation 为 1: Standardization 之前,Normal Distribution 的 Standard Deviation 为 σ. 而 Standardization 之后,这个新的 Standard Normal Distribution 的 x 轴就是本来对应的点与 mean 相差了多少个 Standard Deviation; 本来与 Mean 相差 1 个 Standard Deviation 的数值在转换为 z 之后就会变成了 1.
在 Standard Deviation 之后,本来在不同分布当中的不同数值会按照同一个标准 z 值在 Standard Normal Distribution 出现在 x 轴新的位置。因为这个新的位置会有新的从左端开始算的曲线面积,亦即在总体当中的 percentage, 因此能够进行比较。
Normal Distribution 与 Standardization 并不是犹如平均数般十分直观的概念,在记录这些笔记之前我也考虑过应该怎样叙述才更清楚,最后还是跟着课程本来的阐述顺序。
当初高三的时候只是直接被告知结论,标准正态分布的平均数就是 0 标准差就是 1,当时还是不明就里的。如今明白为何要将一个分布进行标准化,以及那些数字是如何得出来,感叹当时能明白的话就太好了,以及还是要积累才能有更深刻的了解。

