这是给自己看的描述统计学笔记,第四课数据差异,Variability.
上一课讲了如何用一个数字来表示一堆数据,而这一课就会讲怎样用数字来衡量一堆数据之间的差异;或者说,这堆数据彼此之间比较接近还是比较遥远。
这节课回答的问题是,“怎样来衡量一堆数据的差异程度?”
Data Range 与 IQR
怎样去衡量一堆数据之间的差异程度呢?或者说,这堆数据是相对集中在一起还是相对分散?
最直观的做法还是看看这堆数据的范围在哪里,或者说最大值与最小值之间的差异,即 Data Range. Data Range 大会让人感觉数据很分散,而小的话会让人感觉数据很集中。
例如说一个只有 10 个人的班级,某次考试的分数从低到高排列:
| Score |
| 65 |
| 68 |
| 76 |
| 79 |
| 80 |
| 89 |
| 92 |
| 94 |
| 96 |
| 97 |
这堆分数的 Data Range 就是 97-65=32.
然而单纯看 Data Range 并不可靠。如果另外一个班级都是 90 分以上,只有一个人连 60 分都不到,那么 Data Range 就可能会超过 40, 看上去比上面这个班级的分数更加分散; 然而除去这个不到 60 分的人的话,其他人都在 90 分以上,分数其实相当集中。
因为 Data Range 的这个会被 Outlier 严重影响的问题,看数据的时候可以去除头尾的 25% 只看中间的 50% 的数据,观察这个中间 50% 的 Data Range. 因为每一个 25% 叫做 Quartile, 所以这个中间 50% 的 Data Range 为 IQR, Inter Quartile Range.
再次看回上面的数据,从低到高排列的话,排在 25% 的数字为 Q1 (Quartile 1), 50% 为 Q2, 75% 为 Q3. 虽然 10 的 25% 不是整数,不过也没必要纠结这个:
| Score | Quartile |
| 65 | |
| 68 | |
| 76 | Q1 |
| 79 | |
| 80 | Q2 |
| 89 | |
| 92 | |
| 94 | Q3 |
| 96 | |
| 97 |
这个时候,IQR = Q3 – Q1 也就是 94-76=18. 这个当然比 Data Range 要小了,然而相对来说更加能表示一堆数据的分散程度。例如说上面只有一个人低于 60 分的班级,用 IQR 的方法能去除这个 60 分的 Outlier, 最终的 IQR 不会大于 10, 看起来也更加符合他们的数据比较集中的现实。
IQR 当中大约会有 50% 的数据(毕竟也会有除不尽的时候),不一定会受到每个数据变动的影响,然而却不会受到 Outlier 的影响。顺带说一句,通常 Q2 的数字就是整堆数据当中的 median.
其实平时工作当中要计算访问的时长,直接算个平均分是有问题的,因为总会有人的访问做得很长。这个时候业内惯常的做法是去除头尾 20%, 只用剩下的 60% 来算平均分。Excel 当中的 TRIMMEAN 函数计算这个很方便。
Outlier 的判定
自从上一课开始 Outlier 就不断出现了。究竟怎样算作是 Outlier 怎样不算是,统计学上面惯用的判断方法是:
小于 Q1 – 1.5IQR, 或者大于 Q3 + 1.5IQR
用上面那 10 个人的分数来算的话,那要小于 49 分和大于 121 分的才算是 Outlier; 或者说这堆数据没有十分出位的成分。
其实平时少不了会接触到 Outlier 的判定,而这次也算是有个通用的方法来决定了。当然不同场合会有不同的判定标准,然而至少有个起始的地方。
Boxplot
用文字来表达 IQR 显得有些薄弱;通常来说用来表示 IQR 的图表是 Boxplot. 上述的数据用 Boxplot 表现出来就是:
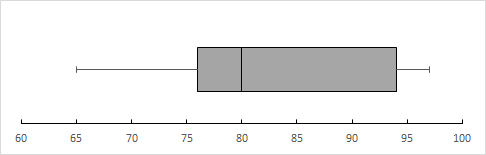
(用 Excel 绘制 Boxplot 的方法可以看这里)
从 Boxplot 可以看出一群数据的最小值,Q1, Q2/Median, Q3 以及最大值的位置。第一条线段是最小值到 Q1, 第一个方框是 Q1 到 Q2/Median, 第二个方框是 Q2/Median 到 Q3, 第二条线段是 Q3 到最大值。
如果有 Outlier 的话可以用一个点将其表现出来,不过上面的示例数据并没有 Outlier.
可以看出来一堆数据的 Median 必然在 IQR 当中,毕竟 Median 的定义就是排在中间的数字。然而 Mean 并不一定,毕竟有 Outlier 的存在的话 Mean 就会变得十分的飘忽了。
从 Deviation 到 Standard Deviation
正如上面所说,无论是使用 Data Range 或者是其改良版 IQR 来衡量数据的差异程度都存在容易受 Outlier 的弊端。从另外更加数学的角度来衡量的话则是 Deviation.
Deviation 是每一个数据与 Mean 之间的差,而且必定是“每一个数据减 Mean”而不能反过来(因为要衡量每个数据与 Mean 之间相差多少),即:
![]()
对上面的分数算 Deviation 的话就是:
| Score | Deviation |
| 65 | -18.6 |
| 68 | -15.6 |
| 76 | -7.6 |
| 79 | -4.6 |
| 80 | -3.6 |
| 89 | 5.4 |
| 92 | 8.4 |
| 94 | 10.4 |
| 96 | 12.4 |
| 97 | 13.4 |
单纯知道这些 Deviation, 或者说每一个数据与 Mean 之间相差多少,并不能衡量数据之间的差异程度。毕竟,这些 Deviation 一加起来就会变成 0, 不能看出什么信息。
(至于为什么等于 0, 那就是因为“每一个数据减 Mean”加起来,就是“每一个数据加起来”减去“每一个 Mean 加起来”就是 0 了)
因为 Deviation 有这样的不足,Absolute Deviation 就出来了,就是 Deviation 的绝对值:
![]()
| Score | Deviation | Absolute Deviation |
| 65 | -18.6 | 18.6 |
| 68 | -15.6 | 15.6 |
| 76 | -7.6 | 7.6 |
| 79 | -4.6 | 4.6 |
| 80 | -3.6 | 3.6 |
| 89 | 5.4 | 5.4 |
| 92 | 8.4 | 8.4 |
| 94 | 10.4 | 10.4 |
| 96 | 12.4 | 12.4 |
| 97 | 13.4 | 13.4 |
对每一个数据的 Absolute Deviation 再来计算它们的 Mean, 是衡量数据差异的一个方法:
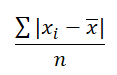
这堆 Absolute Deviation 算出来的 Mean 是 10.
同时除了取绝对值之外,另外一个去除 Deviation 负号的方法是将其平方,出来的结果就是 Squared Deviation. 同样,对这些 Squared Deviation 求 Mean, 则是衡量数据差异的另一个方法:
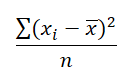
| Score | Deviation | Absolute Deviation | Squared Deviation |
| 65 | -18.6 | 18.6 | 345.96 |
| 68 | -15.6 | 15.6 | 243.36 |
| 76 | -7.6 | 7.6 | 57.76 |
| 79 | -4.6 | 4.6 | 21.16 |
| 80 | -3.6 | 3.6 | 12.96 |
| 89 | 5.4 | 5.4 | 29.16 |
| 92 | 8.4 | 8.4 | 70.56 |
| 94 | 10.4 | 10.4 | 108.16 |
| 96 | 12.4 | 12.4 | 153.76 |
| 97 | 13.4 | 13.4 | 179.56 |
这堆 Squared Deviation 算出来的 Mean 是 122.24. 这个数字很重要,叫做 Variance.
Variance 是平方之后加起来的数字,所以单位也是平方之后的单位。例如上面的是分数,Variance 之后就是“分数的平方”。为了回到本来的单位,需要对 Variance 开平方:
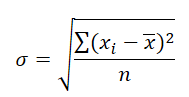
这个就是传说中的 Standard Deviation. 它是最常用的衡量数据差异程度的数值,用 σ 来表示。Standard Deviation 越小,表示数据越集中;反之则然。
对上面的 Variance 122.24 算平方根的话就是 11.06 了。
Standard Deviation 的神奇之处与 Bessel’s Correction
说起 Standard Deviation, 就要说起在一个 Normal Distribution 正态分布当中,以 Mean 为中点,数据有着这样的分布规律:
- 有 68% 的数据在距离 Mean 左右各一个 Standard Deviation 的距离当中
- 有 95% 的数据在距离 Mean 左右各两个 Standard Deviation 的距离当中
- 有 99.7% 的数据在距离 Mean 左右各三个 Standard Deviation 的距离当中
用个图像来表示就是(来自维基百科):
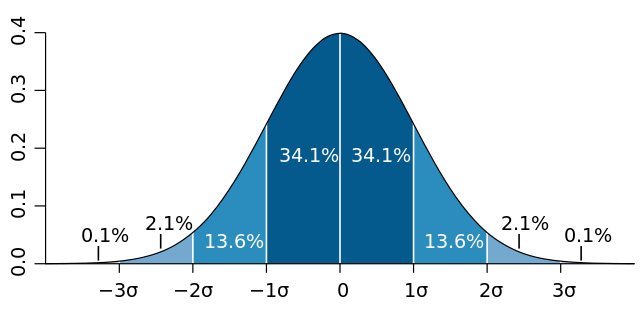
深蓝区域是距平均值小于一个标准差之内的数值范围,在正态分布中,此范围所占比率为全部数值之68%;两个标准差之内(深蓝,蓝)的比率合起来为95%;三个标准差之内(深蓝,蓝,浅蓝)的比率合起来为99.7%。
所以要掉出左右各三个 Standard Deviation 这个范围的话还真的是很低的概率。
正因为如此,如果是对一个总体取样的话,取出来的样本十分可能会在这左右两个或者三个 Standard Deviation 之间(分别为 95% 与 99.7%)。也就是说,这些样本的集中程度,会因为很难涵盖到剩下的 5% 或者 0.3% 而比起本来的总体要更加集中;或者说,样本的 Standard Deviation 会比总体的要小。
这个时候,如果是计算样本的 Standard Deviation 的话,为了使其变得更加贴合总体本来的情况,就需要用 Bessel’s Correction 在计算 Variance 的时候就给分母(样本的数目)减 1 来增加最后 Standard Deviation 的值。
样本的 Standard Deviation 用 s 来表示,那就是:
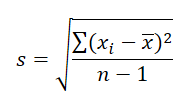
Excel 当中也有 STDEV.P 与 STDEV.S 两个不同的函数来分别计算总体与样本的 Standard Deviation.
当 n 变大之后,其实减去 1 出来的结果与不减并没有多少区别了。换句话说,样本数目越大的时候对总体的衡量程度愈发精准了。
其实 Standard Deviation 的概念在初中三年级就已经遇见过了。然而当时并没有考虑到总体与样本之间的差异,直到现在接触了正态分布与概率论之后才明白为什么需要 Bessel’s Correction 来校正所得出来的 Standard Deviation.
其实目前的课程内容难度还是比较低,不过依然还是会有新的认知与感悟;毕竟这次这么认真地上这个课程,是为了认真打好统计学的基础啊。

