给自己看的笔记-描述统计学-03 集中趋势

这是给自己看的描述统计学笔记，第三课集中趋势，Central Tendency.

本来以为是讨论中央定律之类的，然而最后却只是在讨论平均数、众数与中数而已。

这节课回答的问题是，“怎样用一个数字来描述一堆数据？”

之前的课程：第一课 第二课

 

Measure of Center

要是只用一个数字来描述整个数据集的话，通常有三种选择：

• Mode 众数，在一个数据集当中出现次数最多的数字
• Mean/Average 平均数，这个人尽皆知的数据集总数除以数据集当中的数据数目
• Median 中数，从大到小或者从小到大排列一个数据集然后排在中间的数字

 

Mode 众数

众数就是一个数据集当中出现最多的那一个，能够看出数据当中最可能出现的值是什么。

乍眼一看很简单，其实还有一些我之前都没有留意到的性质：

• 可以不是一个具体数值，在 histogram 当中则是作为 frequency 最大的那个 bin. 因此，mode 会跟随 bin 的大小而改变。
• Mode 可以有多个，这个容易理解；Mode 可以不存在，如果所有数值或者 bin 的 frequency 相似的话。
• Mode 可以用来描述数值 numeric,也可以描述名称 categorical. 例如说，男性的数量比女性要多的话，那么男性就是 mode.
• Mode 必然是 histogram 上面 X 轴的内容，不能是 Y 轴上的。
• 样本的 mode 和总体的 mode 不一定一样，这个是抽样的时候就决定的了。
• 新增加一个 outlier 并不影响 mode.

 

Mean 平均数

Mean 表示数据集的均衡点，能反应整个数据集的表现。例如说算不同班级的考试表现，通常用的是平均分而不是其他。

地球人都知道平均数怎么算，用公式来表示一下的话就是：

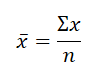
或者是：

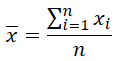
同样，样本的 mean 与总体的 mean 也不一定一样。不过新增加一个 outlier 将会十分影响 mean 的数值。

 

Median 中数

把一串数值从小到大或者从大到小排列出来，在中间的那个就是 median 了。这个数很特别，比它大的数据数量，与比它小的数据数量是一样的，所以与最大最小值一起，能初步感觉数据集的分布情况。

数据集有奇数个数据的时候，median 就是：

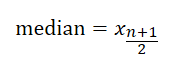
而偶数个数据的时候，median 就是：

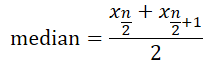
Outlier 的存在对 median 影响不大，反正多一个不多少一个不少。

 

总结

以下为这三个数值不同性质的简表：

	Mean	Median	Mode
能用公式计算	Y	Y
任何数据变动都会导致改变	Y
不受 bin 大小影响	Y	Y
不（大幅）受到 outlier 影响		Y	Y
容易在 histogram 当中看出来			Y

而且，在一个 positive skewed 的 histogram 当中，这三个数值的关系为 mode < median < mean; negative skewed 的话则是反过来 mean < median < mode. 如果正好是 normal distribution 的话，这三者是一致的。

 

这次的笔记不用 Bamboo Page 改为用 OneNote, 发现效果好了很多。

Banboo Page 限制了笔画的粗细，而且写下来的内容不能移动，页面也只有屏幕那么宽。相比之下 OneNote 无论是普通笔还是荧光笔都能自由调整色彩与粗细，还能移动已经写下的内容可以再排版看起来不会那么混乱，手写的英文的话还能进行搜索，最后还有逆天的公式编辑器，加上同步功能，一款免费的产品做到这份上已经很让人满足了。

尤其是，自己在选择笔画粗细的时候，看到标注的那个 0.5 毫米粗细正是自己最喜欢的实体笔，那一刻还是很惊喜的。